Fantasy engineering: A public transport plan for Livingston and Bathgate

A public transport plan for Livingston and Bathgate

This isn’t really a plan for improved public transport in Livingston and Bathgate, although if anybody wants to build it, I’d appreciate five per cent. This is a post about me spending a few idle days making a schematic map to keep myself amused. I have long found the maps and drawings associated with railways to be fascinating things, and every now and then I simply have to stop whatever else I am doing and draw some trains.

Livingston and Bathgate are a built up area in the county of West Lothian in central southern Scotland. Their total population is 78,000. The geology of the region means that although there are two passenger railways running east to west, both miss the built-up areas, and communication from south to north through both towns is not very good. One railway line from Edinburgh to Glasgow runs to the north of Livingston and Bathgate, the second line runs to the south of it, and the line to London (Euston, not King’s Cross) runs farther south than both. I had a go at planning an improved public transport network.

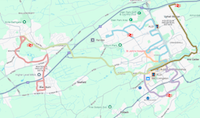
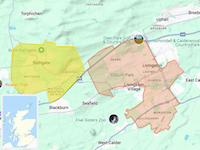Firstly, this is where Livingston and Bathgate are. They’re in between Edinburgh and Glasgow, in the county of West Lothian, Scotland. Originally they were mining towns, in the part of south Scotland that spent the first half of the twentieth century mining shale rock and extracting the oil from it.

↑ Click on the thumbnails to enlarge them.

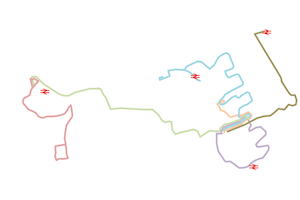
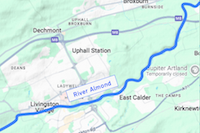The river Almond runs through Livingston and just south of Bathgate. It has recently been cleaned up and made into a place of beauty. I thought at first that it might make a commuter water-bus route, but thinking about it I felt that the traffic for a water-bus service would probably be tourist traffic. Indeed there might be a heavy demand for a tourist water-bus service because of the enormous tourist traffic in Edinburgh. So, here is the course of the River Almond with water-bus stops marked. Most of the stops serve the neighbourhoods along the route of the river and are more likely to be used by commuters than by tourists. Each terminus of the proposed route is in green park land, the easterly end in Almondell Country Park, the westerly end in Almondvale Park. There is a stop close to the town centre. These locations will probably carry tourist traffic. Near both termini there are pools wide enough to allow a water-bus to turn, although if there turns out not to be enough room for a water-bus to turn, the alternative is to use double-ended water-buses.

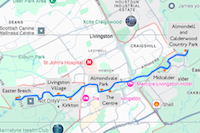Here are possible sites for stops on the riverbanks along the route. I envisage stops being small platforms with shelters on the bank of the river. On fine summer days I expect there to be a considerable number of passengers boarding and alighting at the termini and at the city centre stop. I'm not sure whether stops in the suburbs really serve any useful purpose.

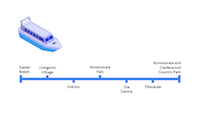This is the first stage finished. I had a water-bus route which appeared to be plausible and feasible, so I expressed it as a schematic. Which makes it look professional, and it's fun to do.

You probably notice that the marks on the schematic which represent stops are not drawn alternately to the left and to the right, as they are on railway and subway maps. Here’s why that is. Normal road buses keep to the left and stop only at bus stops on the left hand side of the road. Water-buses, though, can stop at a platform on either side of the river. In this schematic, the stops are drawn on the side of the river where they actually are. For instance, if you are sailing eastwards from Easter Breich, then Livingston Village is on the port side and Kirkton is on the starboard side.
Assuming that the water-bus can travel throughout the route at 6 mph, which is the speed limit on most British navigable rivers, and stops for 1½ minutes per stop, which is the stop time of the Venice water-buses at most stops, the end to end travel time for the water-bus service stopping at all stops is 48½ minutes, which is conveniently close to the 45 minutes which is often assumed to be the duration of a tourist’s attention span. A water-bus travelling end to end, stopping only at the City Centre en route, will take 40 minutes. Thus one water-bus can provide a service every two hours, and two water-buses can provide one service per hour, and the journey is long enough to make it possible for meals to be served on board.

Now I moved on to workaday transport services. I decided that a good way to transport people north to south in Bathgate and Livingston would be by trolleybus. They offer higher speeds and lower noise and pollution than diesel buses. They are slightly more expensive (I saw an estimate of 20% more) than diesel buses because overhead catenary has to be installed, but they are far easier to instal in a built-up area than a new railway or a new metro, which require very expensive tunneling or extensive demolition to create railway corridors. The often canvassed urban monorail also needs demolition in order to install the columns which support its track, and in addition the design of the network of monorails is difficult because junctions are cumbersome.

I drew a network of six routes which appeared to bring most of the residences in Bathgate and Livingston within a quarter of a mile (five minutes’ walk) of a trolleybus stop. In my mind, I had an image of a modern single deck trolleybus rather than the London double deck trolleybuses of legend.

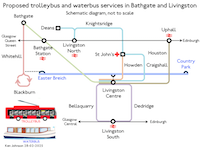
Take away the buildings and what is left is the trolleybus routes. I re-drew the diagram of routes, replacing bent and wiggly lines by straight lines, and the result was…

…the final schematic, showing the trolleybus routes, the waters route, the railways and drawings of a trolleybus and a water-bus. Click to enlarge.

How to fix inflation

It is fashionable for wannabe Government Ministers and so forth to tell us that they want to bring inflation down, and the only way they can think of bringing it down is increasing the mortgage interest rates — which, as Christopher Robin observed, hasn’t worked yet. For some reason the idea of cutting the prices of food, gas and electricity by fiat doesn’t seem to occur to them. In the long run, and quite possibly in the short run as well, increasing mortgage interest rates will cause thousands of deaths as people starve and freeze to death in unlighted houses, or on the streets. Another way to take money out of the economy, which is the ostensible purpose of raising mortgage interest rates — nothing to do with giving our chums in the banks huge bonuses, honest, Guv’nor — has to be found fast.

Therefore, I am posting an alternative way to take money out of the economy. Bring back the sixpence.

If every household in the UK were to save sixpence a week in a piggy bank, that would take more than £36 Mn out of the economy in every full year. (28.2 Mn households × 52 weeks × 6d = £36.66 Mn.)

On the other hand a 1% rise in interest rates raises only £16.75 Mn. (£1,675.4 Mn total mortgage debt × 1% = £16.754 Mn.)

Of course, the plan will work only if people want it to work. That’s why I’m not calling for compulsory saving. Under compulsory saving, people feel, rightly, that they can’t get hold of their sixpences should they suddenly need them. So the sixpenny coin has to be psycho-numismatically designed so that people will want to keep it and not spend it, as they did with the old sixpences. ‘Save two new pence and three new pence on alternate weeks’ is arithmetically the same, but doesn’t cut it.

Likewise, people have to not want to take money out of their piggy banks. Fortunately this problem too has been solved. The piggy banks are made of pottery and don’t have an opening for taking the sixpences out. You have to drop it or break it, so usually the coins stay in the piggy bank and they aren’t taken out and spent. Those sixpences are just as far out of the economy as the money you hand to the banks instead of spending it on food and clothing.

What of those who are too poor to save 6d per week? They can save 6d per fortnight. However many people can’t pay the full whack, the total saved in piggy banks will be at least £18 Mn, which is still more than is raised by a 1% rise in mortgage interest rates.

So there you are, Mr Hunt. As Mr Punch would have said, that’s the way to do it. My bill is in the post.

Long distance bike paths

Let’s waste a few million on very long distance bike paths

I no longer seem to be strong enough to ride a bicycle, but I used to cycle often, and occasionally I rode long distances. I went 100 miles from Edinburgh to Newcastle upon Tyne in about 16 hours on one occasion and I rode the organised double marathon from Edinburgh to St Andrews on two others. But for the purposes of this article, one hundred miles is a mere bagatelle. I am writing about bicycle paths that go all the way across Europe.

So, when I learned that the Channel Tunnel has not just the two bores for trains, one in each direction, but also a ‘service tunnel’ which runs the full length of the tunnel and allows access for repair, maintenance and emergency exit, I thought it unfair that cyclists were not allowed to ride through the service tunnel. I still think it is unfair that cyclists are not allowed to ride through the service tunnel — even on days when nobody else is using it — but as the service tunnel is 31½ miles long, riding through it would take your average cyclist two or three hours without rest stops, and there are no toilets or seats along the way, so the ride is an unattractive prospect. Even the 2007 Tour de France, which started in London, did not ride through the tunnel.

Click on the pictures to view the full size versions.

The Channel Tunnel is made up of two railway tunnels and a service tunnel which runs between them and doesn’t take bicycles

Therefore I am not about to found a campaign to have cyclists allowed through the Channel Tunnel, although the addition of lighting and art to the 90 yard Colinton tunnel in south west Edinburgh shows that tunnels can be made into attractive cycle routes. I leave the important duty of opening the Channel Tunnel to cyclists to anyone who wants to take it on.

Colinton Tunnel in Edinburgh has been fitted with lighting and decorated with a mural, and has become a joy to ride through

Instead, I will allow the cyclists to choose between taking their bikes on Eurotunnel (bizarrely, cyclists are banned from the Shuttle unless they have their cars with them) and riding one of the many attractive ferry services which still operate across the English Channel.

The interesting question — to me, anyway — is, if you are going to take a cycling holiday, what dedicated, peaceful, scenic routes are available to you. I found it interesting that since the Middle Ages there has been a network of scenic low speed paths all over Europe. Those are the pilgrimage paths.

Here is a map of the European pilgrimage paths, which for some reason leaves out all the pilgrimage routes in Great Britain and Ireland. I copied this map from Traildino’s web site.

Scenic low speed routes across Europe: the Pilgrimage Paths

Of course, many of these routes are not suitable for cyclists, or at least not suitable for cyclists of average ability riding average bicycles. My point is that there exists a network of low speed, traffic free scenic routes all across Europe, and those paths have existed for centuries. For centuries, therefore, there have been travellers who wanted to go slowly and enjoy the journey, rather than to arrive at the end of the path as quickly as possible. There is actually a need for slow roads as well as fast ones.

All over the world for the last hundred years or so, Ministers of Transport have encouraged faster and faster cars by building faster and faster roads, yet we have ended up with cars which spend nearly all their time (96·4% according to Reinventing Parking) standing outside their owners’ houses impressing the neighbours. Do things have to be this way? Can’t we look again at the possibility of making travel a pleasure?

Of course, making travel a pleasure does not just mean building cycle paths, as hikers, ramblers, passengers on many steam railways and those drivers who rattle around the streets in vintage cars will probably agree. It means that over the next hundred years those same Ministers could gradually, incrementally, construct a bike path network of long distance paths. I mention the hundred years because that is how long it has taken the Netherlands to construct the spectacular cycle provision which it has today. Whatever the people who installed cycle routes in completely unsuitable places in Edinburgh may think, it takes years for an attractive, usable network of bicycle paths to develop.

What can we expect of a long distance bike path

A long distance bicycle path needs to be:

1. Continuous. The design of a path needs to allow for very young cyclists. Any interruption to the path, for example expecting the rider to dismount and walk across a busy road, or operate a traffic light, or cycle along a busy road for half a mile, renders the path useless or even worse to small cyclists.

2. Level or gently graded. Fortunately, this too has been done before. The flight of locks at Caen Hill on the Kennet and Avon canal rises 237 feet over two miles, which is a gradient of 1 in 44½. It is the steepest gradient of any canal in Britain. The railways regard 1 in 50 as a steep gradient. Hills are one of the most effective deterrents to cycling, and bike paths should avoid them by taking paths along flat (ish) landscape features like rivers, canals, coasts and railway lines.

What is noticeable here is the similarity of a gradient regarded as steep by two completely different means of transport. It gives me confidence that the steepest acceptable gradient on a long distance bicycle path will turn out to be 1 in 50.

3. Away from big roads. The bike lanes recently built in Edinburgh, like the one on Crewe Road North, in the picture, miss the point of cycling. The paths are built along the edges of busy roads, instead of supporting the use of old railway lines, canal towpaths, footpaths and back streets, all of which Edinburgh has in large numbers. Cycle lanes are never swept or gritted in winter, are often blocked by parked cars and leave the riders inches away from cars which almost always defy the speed limit. The idea of imposing a low speed limit in order to protect cyclists doesn’t seem to have occurred to anybody, and wouldn’t work even if it had. Motorists regard obeying a 20 mph speed limit as a ridiculous thing to expect them to do.

4. Close to services. Long distance bike paths are too long to cycle end to end, out and back in a day, carrying everything you need. You need bicycle parks, border posts, cafés, cash dispensers, chip shops, drinking fountains, fizzy drink dispensers, hostels, hotels, picnic tables, postcard vendors, police posts, pubs, restaurants, schools (you don’t really need those along the bike path but it’s a good place to build them, because they offer safe access on foot as well as by bicycle,) shelters, sweet shops, telephone boxes and shops offering bicycle hire, repairs and spares.

Those would make the paths interesting, useful and lively places near cities.

5. Lit at night, swept regularly, gritted in winter and free from parked cars. (The picture shows the Pescara Path, in eastern Italy, at night.)

6. Free to use.

 

Where will the long distance paths go?

I found myself eager to draw at least one map. I drew it because I like drawing maps. This map is only conceptual: it is not supposed to form part of any project. The paths shown on it are the V1 (2800 miles,) V2 (1400 miles) and V3 (2600 miles.) I chose the letter ‘V’ to stand for ‘Velocipede,’ a word which exists in pretty much every European language except, I think, Basque, Hungarian and Welsh. Numbering the bicycle paths systematically is the least of the problems. They could instead be named after men and women who have performed some meritorious service, like ‘Kenneth Johnson Way.’

While I’m on the subject

Building a level (or almost) path across open countryside may be easier and require less earth moving if the path shares the route of some utility which is level anyway. But you have to share it in a way which does not expose cyclists to the risk of being struck by a car or a train. This is how to lay a cycle path beside a canal or a river, beside a railway, or beside a main road.

If there is no alternative to taking the cycle path along a road that passes through a built-up area, here are a bad way to do it and two good ways.

Do not do this. Sooner or later it will kill someone.	Cyclists ride on extended pavements, one on each side of the road	Cyclists ride in both directions on an extended pavement

It is better to route cyclists away from the main road. If there is no convenient railway, river, canal or other route which can be used for traffic free cycling, then maybe you can create a cycle route along back streets where there is little traffic and it doesn't go very fast. As an example, in the old council housing estate at Craigmillar there is a back street route which avoids the main road. In the more recently built Niddrie Mains estate, because the designer felt the need to avoid creating ‘rat runs,’ there is apparently no back street route along which to continue it.